How I calculated the 1,000,000th Fibonacci Number with Python

Note, this article was originally uploaded to Medium.

No, the title is not clickbait at all! A few days ago I really wanted to find the optimal solution to calculating Fibonacci numbers and I wanted to try to calculate the 100,000th number in the sequence, but I thought; if I could calculate the 100,000th, what’s stopping me finding the 1,000,000th? So today, I am going to show you how I went about doing this and all the issues I came across.

The Fibonacci sequence is one of the most well known mathematical sequences and is the most basic example of recurrence relations. Each number in the sequence consists of the sum of the previous two numbers and the starting two numbers are 0 and 1. It goes something like this:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and so on forever..

Over the next few minutes, I will go through a few different approaches until I show you the optimal solution:

1. Using simple recursion
2. Using cache with recursion
3. Using an iterative method
4. Using Binet’s formula
5. Calculating the 1,000,000th number

But before we get started, I must say that all the timings mentioned are all based on the hardware I am currently running and the Python version (3.9.1).

Using simple recursion

This is a very simple and easy way to return the nth Fibonacci number in Python:

# fibonacci.py

def recursiveFib(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFib(n - 1) + recursiveFib(n - 2)

It uses recursion to repeatedly call itself multiple times calculating the previous number and using it to work out the next. But that is also its downside, as the function extremely inefficient and resource intensive, this is because at every stage it calculates the previous 2 numbers, and the previous 2 numbers of those number etc. Soon you reach a point where it takes too long to calculate the next number, for example on my computer it took me 1.43 seconds to calculate the 35th number. This will obviously be extremely slow, and basically impossible, to calculate higher values.

Using cache with recursion

Since we constantly calculate the previous 2 numbers, we can harness the power of caching to store the number, so we do not need to calculate them anymore. The built-in functools module allows us to use a least recently used cache; a type of cache which organises the items in order of use. This can speed up the process by a huge amount.

# fibonacci.py

from functools import lru_cache

@lru_cache()
def recursiveFibCached(n):
    if n == 1 or n == 2:
        return 1

    return recursiveFibCached(n - 1) + recursiveFibCached (n - 2)

Firstly, we need to import the lru_cache decorator from the functools module and place it before our function. We can supply a maxsize value to tell the cache how many items to store, but by default it is 128 and that works perfectly fine. By using the cache, we can calculate the 200th Fibonacci number in only 0.0002252 seconds!

But one issue with using recursion is that if you try to calculate the 501st number you will get an error as such: RecursionError: maximum recursion depth exceeded in comparison. But thankfully you can get around this issue by setting the recursion depth to something higher:

# fibonacci.py

import sys

sys.setrecursionlimit(5000)

Now we can calculate the 1,000th Fibonacci number, which took me only 0.001198 seconds to compute. However, this created another issue for me, I could not, for some strange reason, calculate the 1,553rd number in the sequence, and even after increasing the recursion limit nothing would happen, nothing would be printed out to the terminal and the program would just simply exit. This is obviously an issue and a drawback on my route to calculate the millionth Fibonacci number.

Using an iterative method

You might see that using a recursive solution to a problem is often seen as malpractice in computer science, instead iterative methods are considered much better. We can create an iterative solution to generate Fibonacci numbers as well:

# fibonacci.py

def iterativeFib(n):
    a, b = 0, 1

    for i in range(n):
        a, b = b, a + b

    return a

We can use this to calculate any Fibonacci number (I have not tested with extremely huge numbers) and it is often extremely fast as well, only taking 0.0028195 seconds to calculate the 10,000th number. You might be wondering why we cannot use this to calculate the 1,000,000th number, and we can, but it will take a bit of time. Keep reading and I will explain this.

Using Binet's formula

Binet’s formula is a formula which can be used to calculate the nth term of the Fibonacci sequence, which is exactly what we want to do, and is named after it was derived by the French mathematician Jacques Philippe Marie Binet. The formula is shown below:

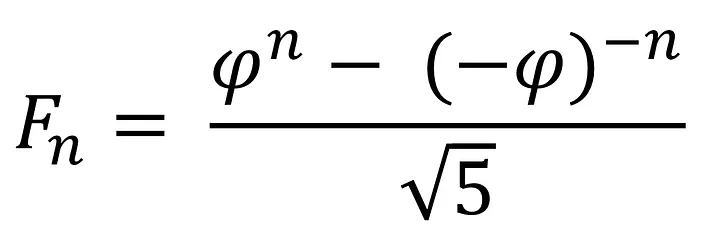
You might notice the Greek letter Phi (ϕ), this is equal to the golden ratio:

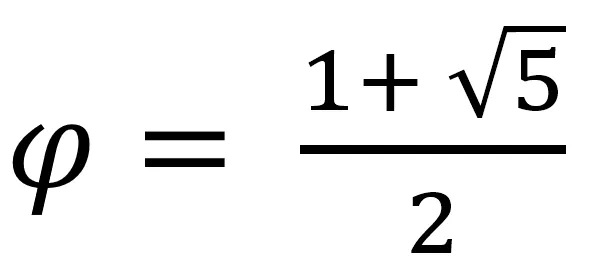
We can convert thing formula into Python and start using it straight away:

# fibonacci.py


def formulaFib(n):
    root_5 = 5 ** 0.5
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

Note for the python implementation we need to return the rounded version of the number we calculate, this is because when we calculate a large number Python will return to us a number where there can be 20+ trailing 9’s after the decimal place. This is all well and good since now we do not have any loops and can instantly compute the answer, right? Well, there is a small catch to this method. If we try to calculate anything above the 1475th number, we will run into an error; OverflowError: (34, result too large). This is due to the way floats are implemented in python and they can only have a certain maximum value, which we exceed using this method.

However, a fix to this is very easy to implement. We can use a built-in module called Decimal to create a decimal object with a much higher precision and size to use in our equation:

# fibonacci.py

import decimal

def formulaFibWithDecimal(n):
    decimal.getcontext().prec = 10000

    root_5 = decimal.Decimal(5).sqrt()
    phi = ((1 + root_5) / 2)

    a = ((phi ** n) - ((-phi) ** -n)) / root_5

    return round(a)

In this new function we set the precision value to 10,000 digits long and we convert our root 5 value into a decimal object value and use that in our equation. This allows us to easily calculate the 10,000th number in the sequence in an astonishing 0.0692986 seconds, a huge improvement over all our previous methods.

Calculating the 1,000,000th number

Now, you might have noticed that using the formula is slower than the iterative solution when n=10,000. This is because in the formula we need to create a Decimal object and use that in our equation, this takes more time than looping over one simple instruction 10,000 times. But this is not the end of the story.

If we increase the number of times we need to loop, this can drastically increase the time it takes for the whole process to complete. At some point, when n is approximately 89200, the time it takes for the iterative solution to compute the answer is equal to the formula, and as n increases above this value, the time it takes for the iterative solution increases at a higher rate compared to the increase of time using the formula.

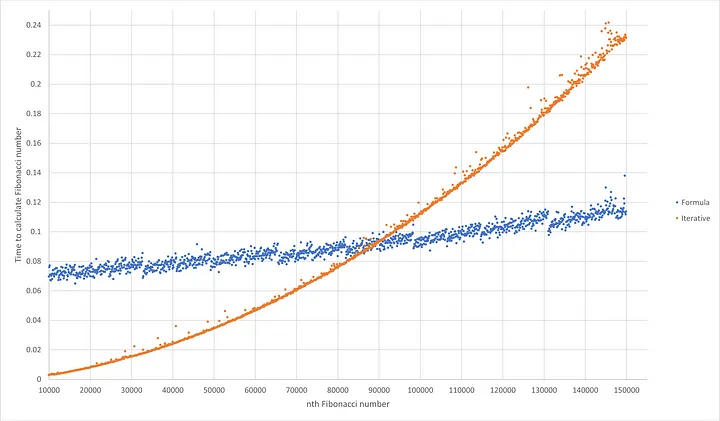
You can see on the graph, the point where the formula and iterative graphs intersect. We can tell from this that as n increases, the time to calculate the Fibonacci number with the formula increases in a linear fashion. But with the iterative solution, the time increases more as n increases more. This makes it clear to us that we need should use the formula to calculate the millionth Fibonacci number. An extra change I had to do to calculate the number correctly was to increase the precision of my Decimal object by using decimal.getcontext().prec = 300000.

On my computer (your times may vary), to calculate the 1,000,000th Fibonacci number it took:

• 8.832661 seconds using the iterative solution
• 1.151380 seconds using Binet’s formula, this is 7.7 times faster!

If you wanted to see the actual number, it is 208,988 digits long and takes 209KB to store in a text file.

Conclusion

So that is how I worked out the millionth Fibonacci number, of course I could work out more but in reality there is no real reason, and it would take a lot of time, even with using Binet’s formula. From the graph above I can estimate that it would take me approximately 310.8467 seconds to calculate the billionth Fibonacci number, but instead I’ll let you do that in your own time.

If you enjoyed the explanation or had any further questions then feel free to leave a comment down below.

Thank you for reading! 💖