Building a Sudoku Solver and Generator in Python (2/3)

Note, this article was originally uploaded to Medium.

Creating the solver

Welcome back to part 2 of this 3 part tutorial, in this section we will create the solver for our sudoku engine, so let’s get straight into the code. But, firstly we need to create two methods which will aid the main solving method.

# sudoku.py

def findSpaces(self): # finds the first empty space in the board, which is represented by a 0
    for row in range(len(self.board)):
        for col in range(len(self.board[0])):
            if self.board[row][col] == 0:
                return (row, col)

    return False

Here we iterate through the board and return the row and column in a tuple of the index position of the first empty square we come across, if there is no square then False is returned otherwise.

Next we will create a method which can check and tell us if a number can be inputted in a certain cell or not:

# sudoku.py

def checkSpace(self, num, space): #checks to see if a number can be fitted into a specifc space; row, col
    if not self.board[space[0]][space[1]] == 0: # check to see if space is a number already
        return False

    for col in self.board[space[0]]: # check to see if number is already in row
        if col == num:
            return False

    for row in range(len(self.board)): # check to see if number is already in column
        if self.board[row][space[1]] == num:
            return False

    _internalBoxRow = space[0] // 3
    _internalBoxCol = space[1] // 3

    for i in range(3): # check to see if internal box already has number
        for j in range(3):
            if self.board[i + (_internalBoxRow * 3)][j + (_internalBoxCol * 3)] == num:
                return False

    return True

This method has two required parameters being a number which is trying to be inputted into a space, which is the second parameter and is a tuple containing a row and column index. The method will first check to see if the number which is trying to be placed in a space appears at all in the same row or column, if it does then that number cannot be placed there and False is returned. Next an internal box 3x3 box is checked and if the number already occurs in the box then False is returned. If nothing is returned so far then the space where we are trying to place the number is deemed valid and True is returned.

Finally, to create the solver we need to think about how we will solve any sudoku board, I created some pseudocode to represent the solving algorithm:

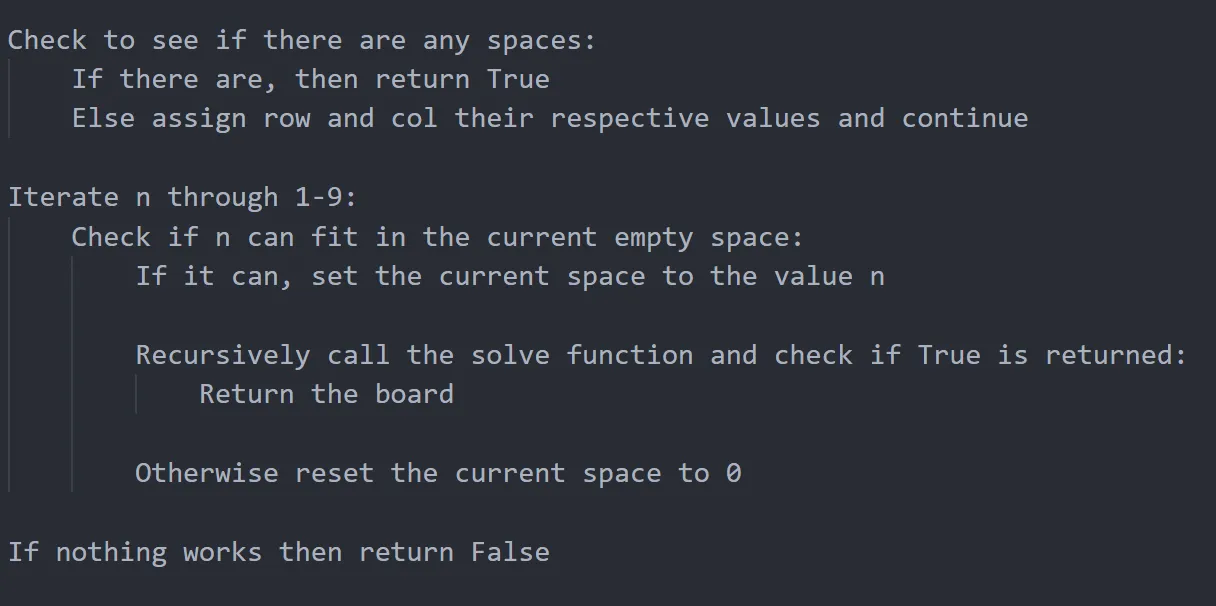
After converting this into python, we get:

# sudoku.py

def solve(self): # solves a board using recursion
    _spacesAvailable = self.findSpaces()

    if not _spacesAvailable:
        return True
    else:
        row, col = _spacesAvailable

    for n in range(1, 10):
        if self.checkSpace(n, (row, col)):
            self.board[row][col] = n

            if self.solve():
                return self.board

            self.board[row][col] = 0

    return False

In this method we will create the solving algorithm which will harness the power of recursion to implement a backtracking solution to complete sudoku puzzles. Firstly, any empty cells are searched for, if there are no empty cells then True is returned as the function has reached its base case, otherwise the function continues.

A for loop then increments the variable n from 1 to 9 inclusive, during each iteration it is checked to see if n can fit in the current empty space, found by the findSpaces method earlier. If it can then that space is populated with the value n and the solve function is recursively called until a base case is reached, which occurs when either there are no more spaces left on the board or no number can fit in the empty space. If the later occurs then False is returned and the board is not returned, instead the space which was previously populated by the value n, is reset to 0 and the for loop continues.

We can also create another method which converts the solved board into a code which can be easily printed out and stored:

# sudoku.py

def solveForCode(self): # solves a board and returns the code of the solved board
    return self.boardToCode(self.solve())

Getting started with generation

To generate a sudoku board which can be filled out as a question, we first need to create a board which is filled of numbers which are fully valid (follow the sudoku rules). To do this we can use a simple little trick and some more recursion to generate a fully populated board. The trick we will use speeds up our generation time by a small amount, but something is better than nothing right? This is how it works:

In this diagram you can see 3 internal boxes in one diagonal line, the contents of the pink box do not interfere with the contents of the blue and green boxes, and vice versa. To start with the generation process we can create a method which generates a fully populated board:

# sudoku.py

def __generateRandomCompleteBoard(self): # generates a brand new completely random board full of numbers
        self.__resetBoard()

        _l = list(range(1, 10))
        for row in range(3):
            for col in range(3):
                _num = random.choice(_l)
                self.board[row][col] = _num
                _l.remove(_num)

        _l = list(range(1, 10))
        for row in range(3, 6):
            for col in range(3, 6):
                _num = random.choice(_l)
                self.board[row][col] = _num
                _l.remove(_num)

        _l = list(range(1, 10))
        for row in range(6, 9):
            for col in range(6, 9):
                _num = random.choice(_l)
                self.board[row][col] = _num
                _l.remove(_num)

        return self.__generateCont()

In the method above we go through each of the 3 internal boxes and populate it with a number 1–9, whilst making sure the number cannot be repicked randomly by removing it from our temporary list of numbers. At the end, the private generateCont method is called, this is so it can fill in the rest of the 54 empty cells on the board. This is what that function looks like:

# sudoku.py

def __generateCont(self): # uses recursion to finish generating a random board
    for row in range(len(self.board)):
        for col in range(len(self.board[row])):
            if self.board[row][col] == 0:
                _num = random.randint(1, 9)

                if self.checkSpace(_num, (row, col)):
                    self.board[row][col] = _num

                    if self.solve():
                        self.__generateCont()
                        return self.board

                    self.board[row][col] = 0

    return False

This method is also recursive since it calls itself during the process of generating a populated board and follows a very similar principle to the solve method. It works by iterating through the board and choosing a random number, and if the current cell is an empty one then it will try and place the number there if it is allowed and then check to see if the board is still solvable. If it is solvable then it will move onto the next cell, otherwise it will reset the value of the cell.

Final thoughts

This was part 2 of the 3 part sudoku solver and generator tutorial, in the next part we will finish off our generator by making sure that only one solution exists for each sudoku created. Make sure to comment any queries and thoughts you have below.

Click here for part 3.

Thank you for reading part 2! 💖